Aus einem Blech der Breite b und der Länge l soll eine Regenrinne gebogen werden, die maximales Wasservolumen aufnehmen kann. Wie muss die Höhe der Regenrinne gewählt werden, damit sich ein maximales Volumen ergibt?
Der Querschnitt der Dachrinne sieht folgendermaßen aus:
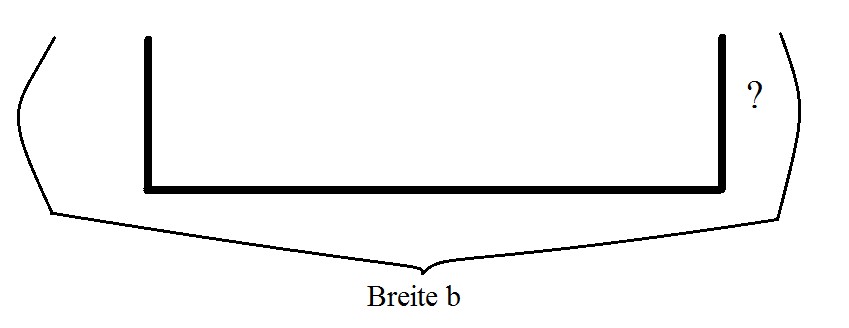
Klicke auf das Dreieck, um einen Hinweis zu erhalten. Versuche aber, ohne die Hinweise auszukommen:
Lege ein Koordinatensystem auf die Skizze und benenne die entsprechenden Längen.
Für die Berechnung der optimalen Höhe ist die Länge der Dachrinne nicht wichtig. Wenn der Querschnitt die maximale Fläche hat, hat auch die Regenrinne das maximale Volumen.
Die halbe optimale Breite der Regenrinne ist: b/4
Kommst du auf dasselbe Ergebnis? Alle Stücke müssen addiert wieder b ergeben.
Die optimale Höhe der Regenrinne ist auch: b/4
Kommst du auf dasselbe Ergebnis?
Vorsicht: Wenn du eine Funktion A(x) zur Bestimmung der maximalen Querschnittsfläche gebildet hast, so ist der Y-Wert des Scheitelpunkts von A(x) natürlich die maximale Querschnittsfläche und nicht die Höhe der Regenrinne.
Falls du den Nullpunkt in die Mitte gelegt hast, hast du beide Seiten berücksichtigt?
Die Höhe der Regenrinne erhältst du am einfachsten aus der Nebenbedingung, oder aus der maximalen Querschnittsfläche geteilt durch deren Breite.
Zusatzaufgabe: Vergleiche das maximale Volumen, das so entsteht, mit dem Fassungsvermögen einer Regenrinne mit halbkreisförmigem Querschnitt. Um wieviel Prozent ist das Fassungsvermögen der halbkreisförmigen Regenrinne größer oder kleiner?
Fertige auch hierfür eine Skizze an. Welche Länge steht für den Halbkreis im Querschnitt zur Verfügung? Für den halben Kreisumfang steht also b zur Verfügung. Was ist dann der Radius des Halbkreises? Und was die Fläche? Vorsicht - alles nur halb. Was braucht man, um eine Halbkreisfläche zu berechnen? Was ist gegeben? Mathematisch gesehen, bedeutet der Vergleich von 2 Größen: Womit muss ich die eine multiplizieren, um auf die andere zu kommen. Die Regenrinne mit U-förmigem Querschnitt ist hier die Bezugsgröße, von der man ausgeht.Hinweis 1z
Hinweis 2z - Spoiler
Hinweis 3z
Hinweis 4z